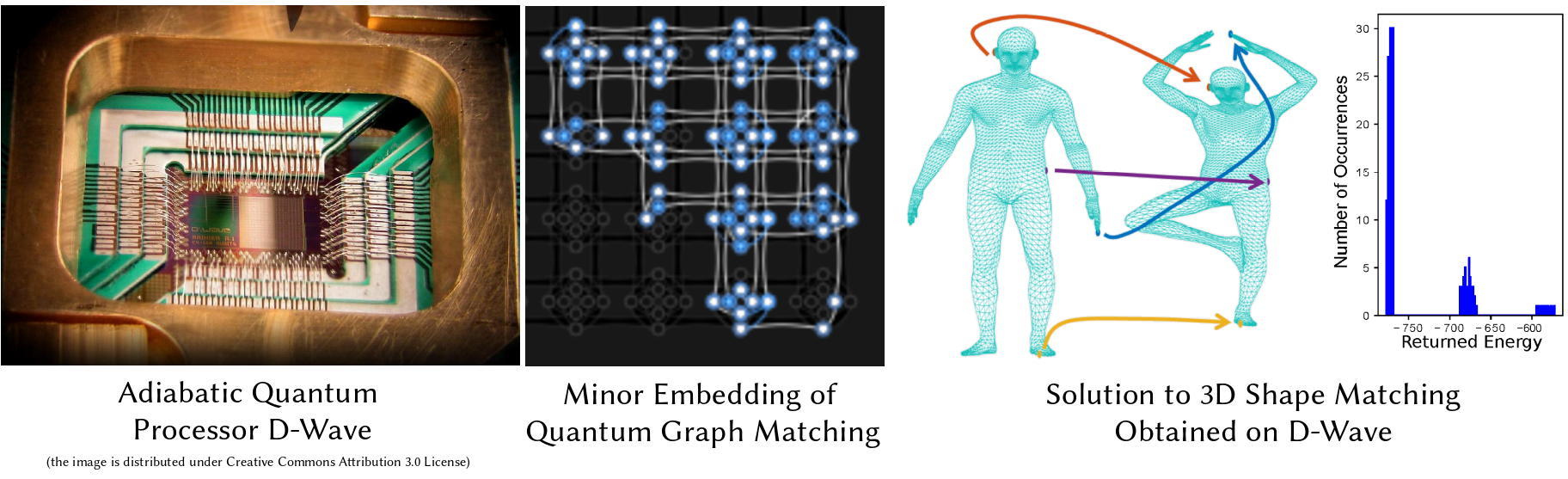
Adiabatic Quantum Graph Matching
with Permutation Matrix Constraints
Abstract
Matching problems on 3D shapes and images are challenging as they are frequently formulated as combinatorial quadratic assignment problems (QAPs) with permutation matrix constraints, which are NP-hard. In this work, we address such problems with emerging quantum computing technology and propose several reformulations of QAPs as unconstrained problems suitable for efficient execution on quantum hardware. We investigate several ways to inject permutation matrix constraints in a quadratic unconstrained binary optimization problem which can be mapped to quantum hardware. We focus on obtaining a sufficient spectral gap, which further increases the probability to measure optimal solutions and valid permutation matrices in a single run. We perform our experiments on the quantum computer D-Wave 2000Q (2^11 qubits, adiabatic). Despite the observed discrepancy between simulated adiabatic quantum computing and execution on real quantum hardware, our reformulation of permutation matrix constraints increases the robustness of the numerical computations over other penalty approaches in our experiments. The proposed algorithm has the potential to scale to higher dimensions on future quantum computing architectures, which opens up multiple new directions for solving matching problems in 3D computer vision and graphics.
Downloads
Citation
@inproceedings{SeelbachBenkner2020,
author = {{Seelbach Benkner}, Marcel and {Golyanik}, Vladislav and {Theobalt}, Christian and {Moeller}, Michael},
title = {Adiabatic Quantum Graph Matching with Permutation Matrix Constraints},
booktitle = {International Conference on 3D Vision (3DV)},
year = {2020}
} Acknowledgement
This work was partially supported by the ERC Consolidator Grant 4DReply (770784).